
Refraction of Light Rays, Examples and Solutions.Reflection of Light Rays, Examples and Solutions.Α n 2, the angle of incidence is smaller than the angle of refraction and so II is also possible. Substitute i by 90 - α in the above inequality to obtain

For what values of α is the incident angle i larger that the critical angle found in part a) above. When light travels through something else, such as glass, diamond, or plastic, it travels at a different speed. When we talk about the speed of light, were usually talking about the speed of light in a vacuum, which is 3.00 x 10 8 m/s. (refractive index of air = 1 and refractive index of water = 1.3)ī) What should be the angle of incidence if we want an angle of refraction not greater than 45 ° ?Ĭritical angle i c = arcsin (1/1.3) = 59 °Īn optical fiber is made up of a core, where light travels, made of glass of refractive index n 1 = 1.5 surrounded by another layer of glass of lower refractive index nĪ) Find the refractive index n 2 of the cladding so that the critical angle at the interface core cladding is 80 °.ī) α is the angle made by the ray with the axis of the fiber. Refraction, Snells law, and total internal reflection 3-20-98 Relevant sections in the book : 26.1 - 26.3 Refraction. Ī ray of light incident in water strikes the surface (assumed flat) separating water from air making an angle of 10 ° with the normal to the surface. For any angle of incidence greater than i c, there is no refraction the ray is totally reflected into the medium of incidence with refractive index n 1. The calculator can also be used to find the value of VSWR using any of the other values. The angle of incidence i c = arcsin(n 2 /n 1 ) is called the critical angle. This VSWR calculator allows you to calculate the reflection coefficient, reflected power, and mismatch loss for a given value of VSWR (voltage standing wave ratio). So when t = 90 ° using Snell's law we write: Let us find a formula for this critical angle of incidence i c. Given angle B calculate angles A, C and D. Given angle A calculate angles B, C and D. Any ray incident at an angle greater than the critical angle will be totally reflected. Rhombus Calculations: The following formulas, based on those above, are used within this calculator for the selected calculation choices. From the table this special incidence angle, called critical angle, is equal to 65.39 °.
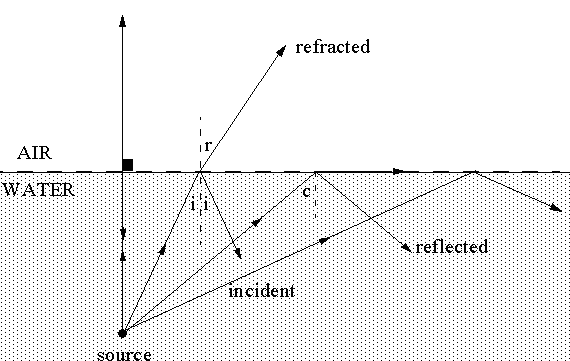
The sine of an angle cannot be greater than 1 t does not existīecause n 1 is greater than n 2, there is a certain angle i for which the angle of refraction is 90 °. Let us make a table of values including different angles of incidence and calculate the angles of refractionĪngle i sin(t) = (n 1/n 2) sin(i) t = arcsin 40 ° 0.70 45.0 ° 65.39 ° 1.0 90.0 ° 75 ° 1.06 Let i be the angle of incidence and t being the angle of refractionĪngle i is the angle of incidence and angle t is the angle of refraction (or transmission). Let a ray of light being incident through a medium of refractive index n 1 = 1.1 onto a medium of refractive index n 2 = 1.0.


 0 kommentar(er)
0 kommentar(er)
